math learning
2017年8月14日 星期一
2016年7月14日 星期四
線性代數重要定理
線性代數自用
對角化出處:http://www.topmath.org/university/alg0702.html
實對稱矩陣可對角化(特徵值為實數)
設 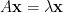 ,
, ,
, 且
且  。等號兩邊同取共軛,就有
。等號兩邊同取共軛,就有  ,再取轉置,
,再取轉置,
因為  是實對稱矩陣,
是實對稱矩陣,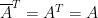 ,便有
,便有
將上式右乘  並代入特徵方程式,等號左邊為
並代入特徵方程式,等號左邊為
等號右邊為 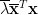 ,合併即得
,合併即得
出處: https://ccjou.wordpress.com/2011/02/09/%E5%AF%A6%E5%B0%8D%E7%A8%B1%E7%9F%A9%E9%99%A3%E5%8F%AF%E6%AD%A3%E4%BA%A4%E5%B0%8D%E8%A7%92%E5%8C%96%E7%9A%84%E8%AD%89%E6%98%8E/
相似矩陣不變性質與證明
性質一:若  相似於
相似於  ,則
,則  與
與  有相同的特徵多項式。
有相同的特徵多項式。
將  代入
代入  的特徵多項式
的特徵多項式 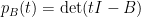 ,就有
,就有
因為特徵值是特徵多項式的根,性質二是性質一的必然結果。
性質二:若  相似於
相似於  ,則
,則  與
與  有相同的特徵值。
有相同的特徵值。
設特徵方程式為 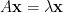 ,以
,以 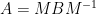 代入上式,
代入上式,
等號兩邊左乘 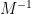 ,
,
雖然  和
和  有相同的特徵值
有相同的特徵值 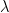 ,但
,但  的特徵向量為
的特徵向量為  ,此即
,此即  參考基底
參考基底 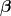 的座標向量
的座標向量![[\mathbf{x}]_{\boldsymbol{\beta}} [\mathbf{x}]_{\boldsymbol{\beta}}](https://s0.wp.com/latex.php?latex=%5B%5Cmathbf%7Bx%7D%5D_%7B%5Cboldsymbol%7B%5Cbeta%7D%7D&bg=ffffff&fg=000000&s=0) 。
。
行列式是所有特徵值的積,跡數 (trace) 是所有特徵值的和,性質三是性質二的必然結果。
性質三:若  相似於
相似於  ,則
,則  且
且 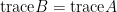 。
。
下一個性質是關於矩陣秩。
性質四:若  相似於
相似於  ,則
,則 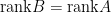 。
。
對任意矩陣左乘或右乘一個可逆矩陣不改變原矩陣的秩,故
下面提供詳細的向量空間分析證明。設 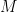 為一可逆矩陣使得
為一可逆矩陣使得  。若
。若 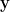 屬於
屬於  的行空間,記為
的行空間,記為  ,即存在
,即存在  滿足
滿足 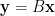 ,則
,則  意味
意味  。換句話說,
。換句話說,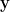 屬於
屬於 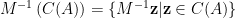 ,推得
,推得
因為 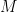 是一可逆線性變換,
是一可逆線性變換, 。所以,
。所以,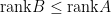 。利用相似變換的對稱性,立知
。利用相似變換的對稱性,立知  。合併上面結果,證明
。合併上面結果,證明  。
。
PS(A的反矩陣B,DET(A)*DET(B)=1)
出處:
https://ccjou.wordpress.com/2010/01/08/%E7%9B%B8%E4%BC%BC%E8%AE%8A%E6%8F%9B%E4%B8%8B%E7%9A%84%E4%B8%8D%E8%AE%8A%E6%80%A7%E8%B3%AA/
行列式相關證明
https://ccjou.wordpress.com/%E6%80%A5%E6%95%91%E6%9F%A5%E8%A9%A2/%E8%A1%8C%E5%88%97%E5%BC%8F/
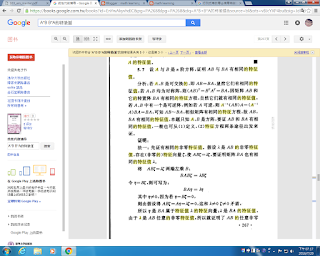
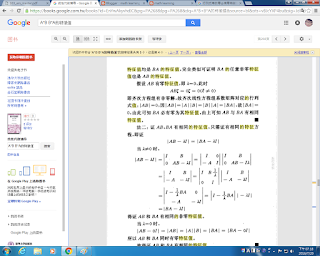
A*B B*A有相同特徵值*****
出處:
https://books.google.com.tw/books?id=EnYwAkyvhdIC&pg=PA268&lpg=PA268&dq=A*B+B*A%E7%9A%84%E7%89%B9%E5%BE%B5%E5%80%BC&source=bl&ots=vBJcYXP4bu&sig=JdlwjlDYCDJ_6rTytM8kqg4oi_o&hl=zh-CN&sa=X&ved=0ahUKEwjCuZvI6oHOAhULG5QKHRxsA2kQ6AEITTAH#v=onepage&q=A*B%20B*A%E7%9A%84%E7%89%B9%E5%BE%B5%E5%80%BC&f=false
Rank相關證明
https://ccjou.wordpress.com/?s=rank
https://ccjou.wordpress.com/2009/09/22/%E5%88%A9%E7%94%A8%E5%AD%90%E7%A9%BA%E9%96%93%E4%B9%8B%E5%92%8C%E8%AD%89%E6%98%8E-rankab%E2%89%A6rank-arank-b/
rank(A*A')=rank(A)
出處:
http://math.stackexchange.com/questions/349738/prove-rank-ata-rank-a-for-any-a-m-times-n
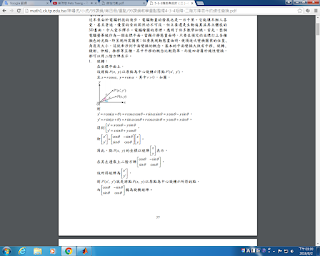
線性轉換旋轉
出處:
http://math1.ck.tp.edu.tw/%E9%99%B3%E5%98%AF%E8%99%8E/%E5%B0%8F%E8%99%8E/99%E8%AA%B2%E7%B6%B1/%E7%AC%AC%E5%9B%9B%E5%86%8A/%E9%87%8D%E9%BB%9E/99%E8%AA%B2%E7%B6%B1%E6%95%99%E5%AD%B8%E9%87%8D%E9%BB%9E%E6%95%B4%E7%90%864-3-4%E7%9F%A9%E9%99%A3-%E4%BA%8C%E9%9A%8E%E6%96%B9%E9%99%A3%E8%A1%A8%E7%A4%BA%E7%9A%84%E7%B7%9A%E6%80%A7%E8%AE%8A%E6%8F%9B.pdf
http://math.nsysu.edu.tw/ezfiles/87/1087/img/495/605.pdf(微分方程聯立方程)
https://zh.wikipedia.org/wiki/%E5%87%B1%E8%90%8A%EF%BC%8D%E5%93%88%E5%AF%86%E9%A0%93%E5%AE%9A%E7%90%86(凱萊定理)

行列式相關證明
https://ccjou.wordpress.com/%E6%80%A5%E6%95%91%E6%9F%A5%E8%A9%A2/%E8%A1%8C%E5%88%97%E5%BC%8F/
A*B B*A有相同特徵值*****
https://books.google.com.tw/books?id=EnYwAkyvhdIC&pg=PA268&lpg=PA268&dq=A*B+B*A%E7%9A%84%E7%89%B9%E5%BE%B5%E5%80%BC&source=bl&ots=vBJcYXP4bu&sig=JdlwjlDYCDJ_6rTytM8kqg4oi_o&hl=zh-CN&sa=X&ved=0ahUKEwjCuZvI6oHOAhULG5QKHRxsA2kQ6AEITTAH#v=onepage&q=A*B%20B*A%E7%9A%84%E7%89%B9%E5%BE%B5%E5%80%BC&f=false
Rank相關證明
https://ccjou.wordpress.com/?s=rank
https://ccjou.wordpress.com/2009/09/22/%E5%88%A9%E7%94%A8%E5%AD%90%E7%A9%BA%E9%96%93%E4%B9%8B%E5%92%8C%E8%AD%89%E6%98%8E-rankab%E2%89%A6rank-arank-b/
rank(A*A')=rank(A)
出處:
http://math.stackexchange.com/questions/349738/prove-rank-ata-rank-a-for-any-a-m-times-n
出處:http://math.stackexchange.com/questions/676333/prove-that-if-ranka-n-then-rankab-rankb
線性轉換旋轉
出處:
http://math1.ck.tp.edu.tw/%E9%99%B3%E5%98%AF%E8%99%8E/%E5%B0%8F%E8%99%8E/99%E8%AA%B2%E7%B6%B1/%E7%AC%AC%E5%9B%9B%E5%86%8A/%E9%87%8D%E9%BB%9E/99%E8%AA%B2%E7%B6%B1%E6%95%99%E5%AD%B8%E9%87%8D%E9%BB%9E%E6%95%B4%E7%90%864-3-4%E7%9F%A9%E9%99%A3-%E4%BA%8C%E9%9A%8E%E6%96%B9%E9%99%A3%E8%A1%A8%E7%A4%BA%E7%9A%84%E7%B7%9A%E6%80%A7%E8%AE%8A%E6%8F%9B.pdf
http://math.nsysu.edu.tw/ezfiles/87/1087/img/495/605.pdf(微分方程聯立方程)
https://zh.wikipedia.org/wiki/%E5%87%B1%E8%90%8A%EF%BC%8D%E5%93%88%E5%AF%86%E9%A0%93%E5%AE%9A%E7%90%86(凱萊定理)

訂閱:
文章 (Atom)